Linear Models

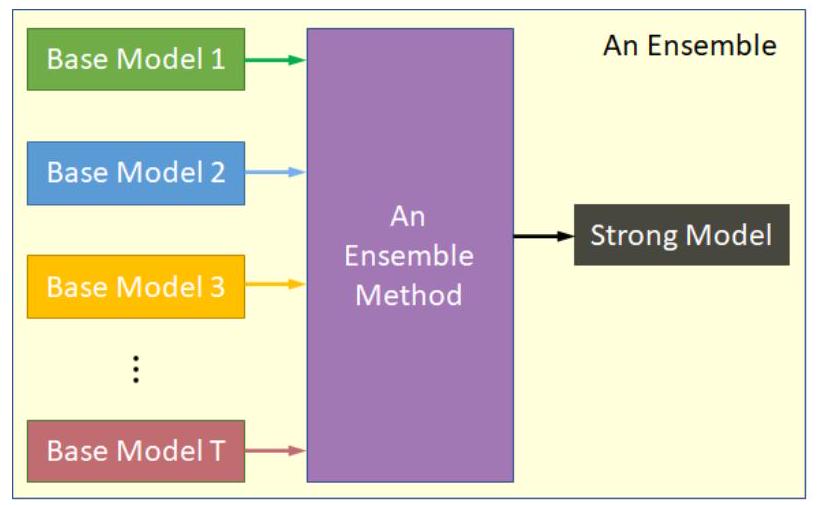
| Sample 1 | Sample 2 | Sample 3 | |
| Model 1 | - | + | + |
| Model 2 | + | - | + |
| Model 3 | + | + | - |
| Ensemble | + | + | + |
| True | + | + | + |
| Sample 1 | Sample 2 | Sample 3 | |
| Model 1 | - | + | + |
| Model 2 | - | + | + |
| Model 3 | - | + | + |
| Ensemble | - | + | + |
| True | - | + | + |
| Sample 1 | Sample 2 | Sample 3 | |
| Model 1 | - | - | + |
| Model 2 | + | - | - |
| Model 3 | - | + | - |
| Ensemble | - | - | - |
| True | + | + | + |



